Rješenje sustava jednadžbi u Microsoft Excelu

Sposobnost rješavanja sustava jednadžbi često može imati koristi ne samo u učenju, nego iu praksi. Istodobno, nisu svi korisnici računala znali da postoje razlike u rješavanju linearnih jednadžbi u programu Excel. Doznajemo kako izvršiti taj zadatak pomoću različitih alata ovog procesora stolova na različite načine.

mogućnosti za rješenja

Bilo koja jednadžba može se smatrati riješenom samo kada se nađu njezini korijeni. U programu Excel postoji nekoliko mogućnosti za pronalaženje korijena. Pogledajmo svaki od njih.

Metoda 1: Matrica metoda

Najčešći način rješavanja sustava linearnih jednadžbi s programskim alatima Excel je korištenje metode matrice. Sastoji se od konstruiranja matrice koeficijenata izraza, a zatim u stvaranju obrnutog matrice. Pokušajmo koristiti ovu metodu za rješavanje sljedećeg sustava jednadžbi:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


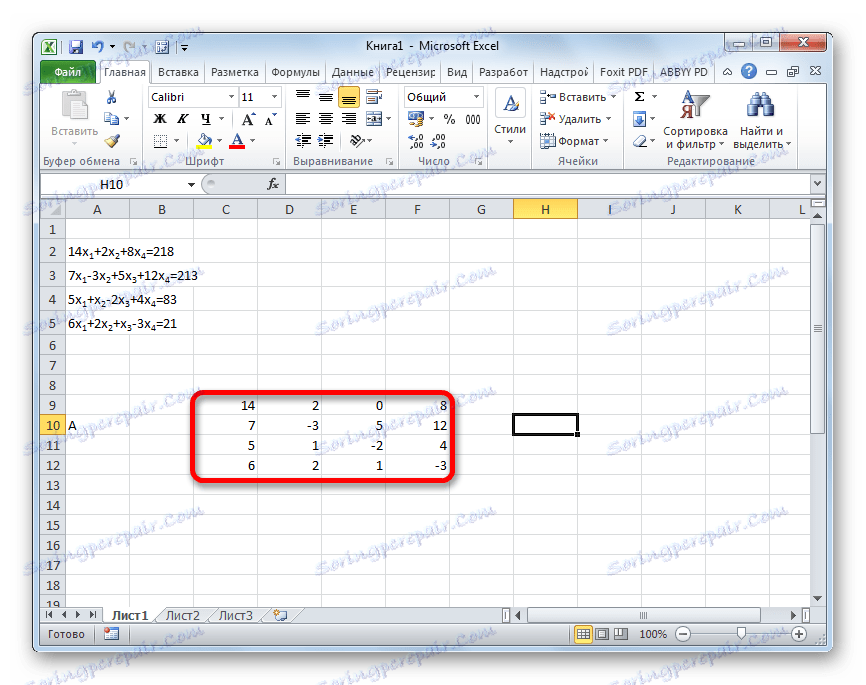
1. Ispunjavamo matricu brojevima koji su koeficijenti jednadžbe. Ti se brojevi moraju redoslijedno poredati uzimajući u obzir mjesto svakog korijena na koji odgovaraju. Ako u jednom izrazu nedostaje jedan od korijena, tada se u ovom slučaju koeficijent smatra jednakom nuli. Ako koeficijent nije naveden u jednadžbi, ali postoji odgovarajući korijen, pretpostavlja se da je koeficijent 1 . Označavamo dobivenu tablicu kao vektor A.
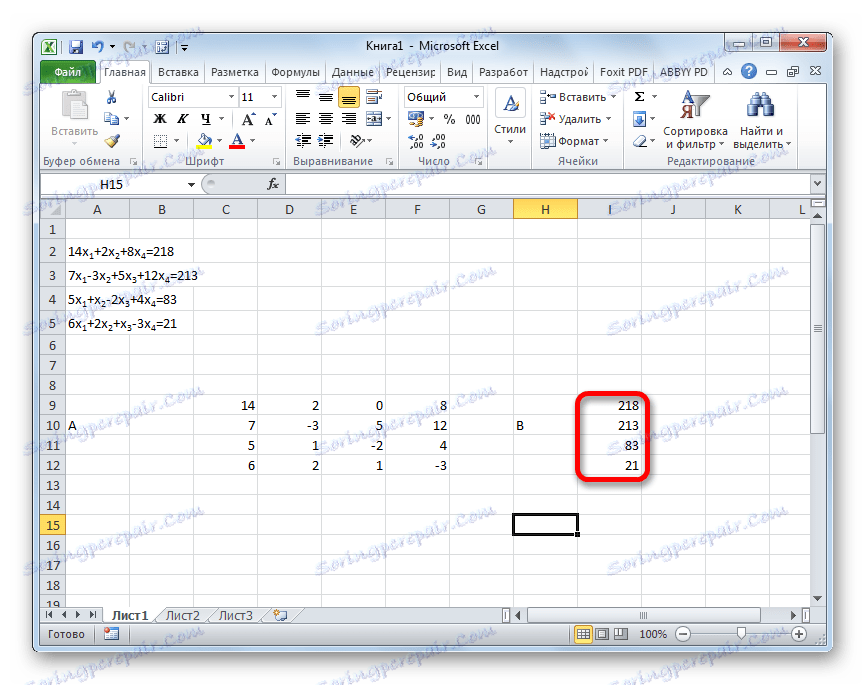
2. Zasebno napisati vrijednosti nakon znaka "jednako". Označite ih njihovim zajedničkim imenom, kao vektorom B.
3. Prije svega, pronaći korijene jednadžbe, moramo pronaći inverznu matricu postojećeg. Srećom, Excel ima poseban operator, koji je dizajniran za rješavanje ovog problema. Naziva se ICBM . Ima prilično jednostavnu sintaksu:

   =МОБР(массив)

   Argument "Array" zapravo je adresa izvornog stola.

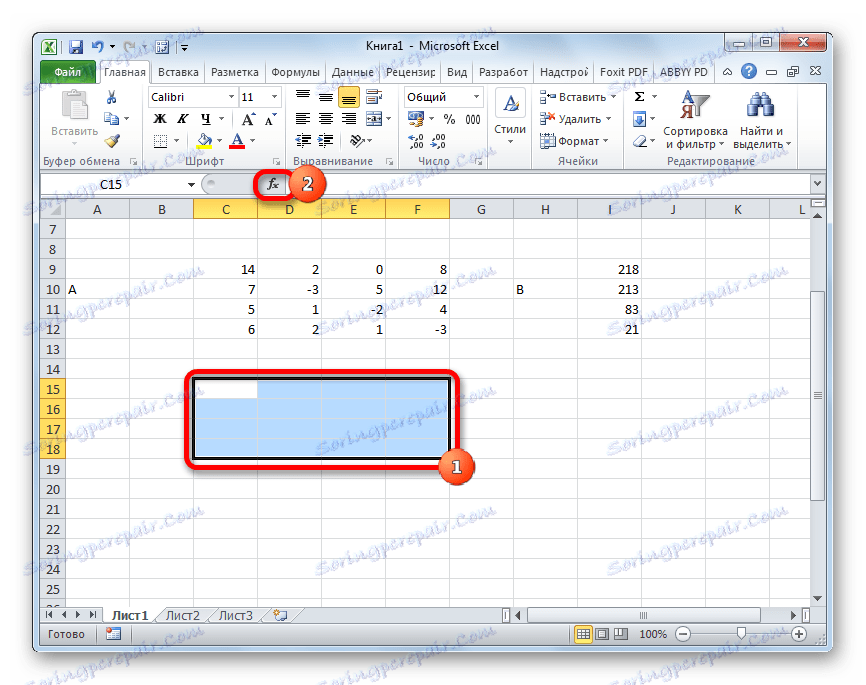
   Dakle, odaberite listu praznih ćelija na listu, koja je jednaka veličini dometa izvornog matrice. Kliknemo na gumb "Umetni funkciju" , koji se nalazi pored linije formule.

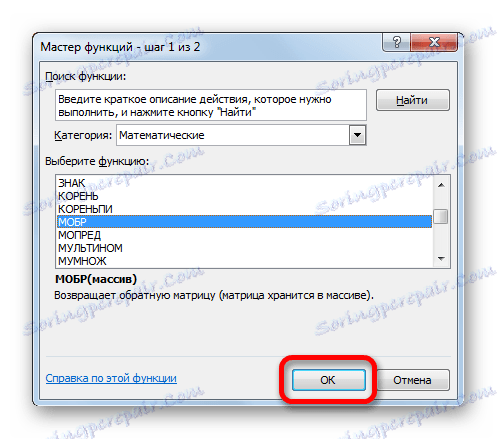
4. Pokreće se Čarobnjak za funkcije . Idemo u kategoriju "Matematički" . Na predstavljenom popisu tražimo ime "MOBR" . Nakon što ga pronađete, odaberite ga i kliknite gumb "OK" .
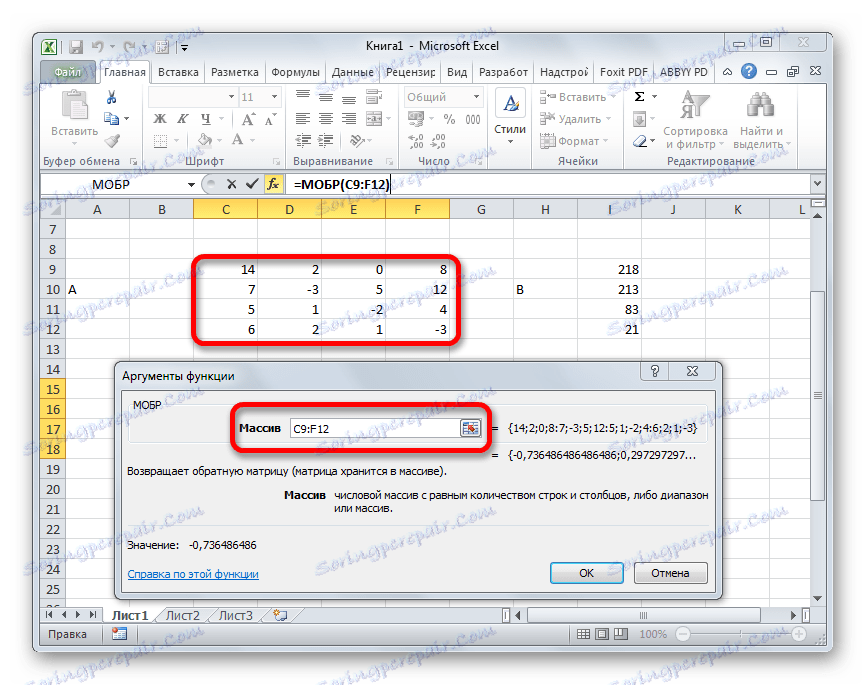
5. Prozor argumenta MOBR funkcije je pokrenut. Ima samo jedno polje u broju argumenata - "Array" . Ovdje morate navesti adresu naše tablice. U tu svrhu postavili smo kursor u ovo polje. Zatim držite lijevu tipku miša i odaberite područje na listi gdje se nalazi matrica. Kao što vidite, podaci o koordinatama lokacije automatski se unose u polje prozora. Nakon završetka ovog zadatka, najočitiji je klik na gumb "OK" , ali nemojte žuriti. Činjenica je da klik na ovaj gumb odgovara korištenju naredbe Enter . Ali kada radite s nizovima nakon što ste dovršili unos formule, ne biste trebali kliknuti gumb Enter , već napraviti skup tipkovnih prečaca Ctrl + Shift + Enter . Mi obavljamo ovu operaciju.
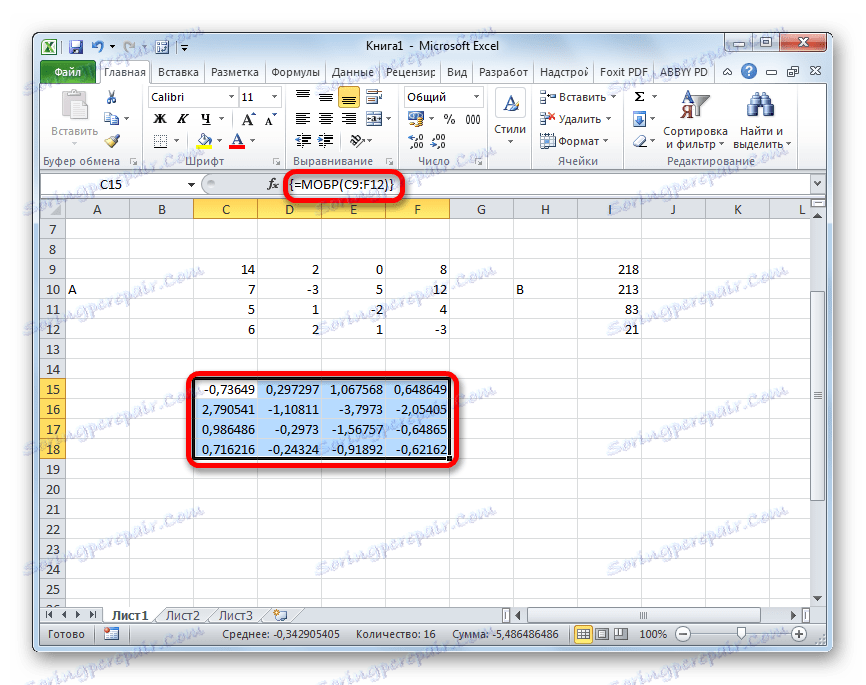
6. Dakle, nakon toga, program izvodi izračune, a na izlazu u prethodno dodijeljenom području imamo matricu obrnuto.
7. Sada moramo umnožiti inverznu matricu pomoću matrice B , koja se sastoji od jednog stupca vrijednosti koji se nalaze nakon jednakog znaka u izrazima. Za umnožavanje tablica u Excelu postoji i zasebna funkcija, koja se naziva HUMAN . Ova izjava ima sljedeću sintaksu:

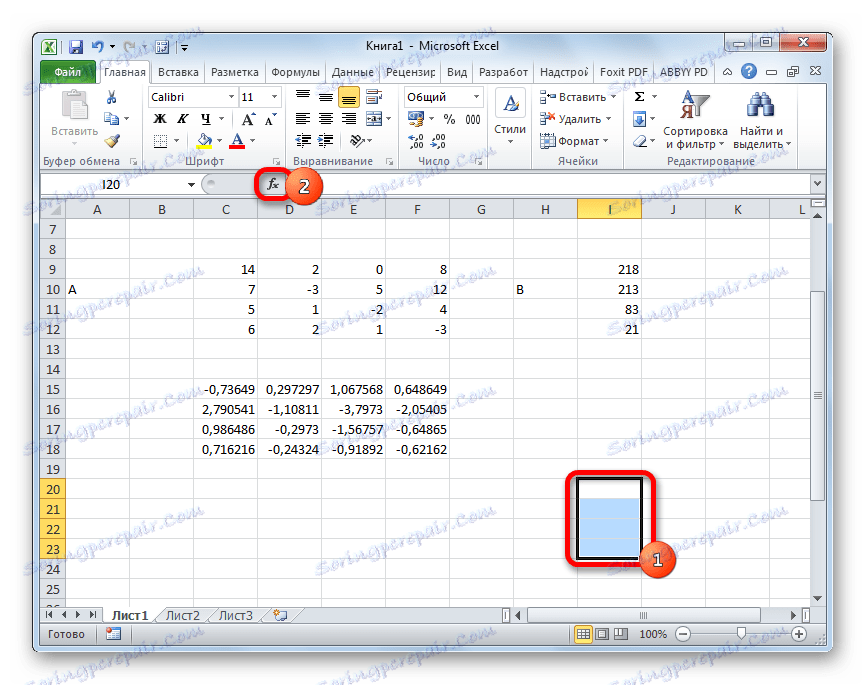
   =МУМНОЖ(Массив1;Массив2)

   Odabrali smo raspon, u našem slučaju koji se sastoji od četiri ćelije. Zatim ponovno pokrenite Čarobnjak za funkcije klikom na ikonu "Umetni funkciju" .

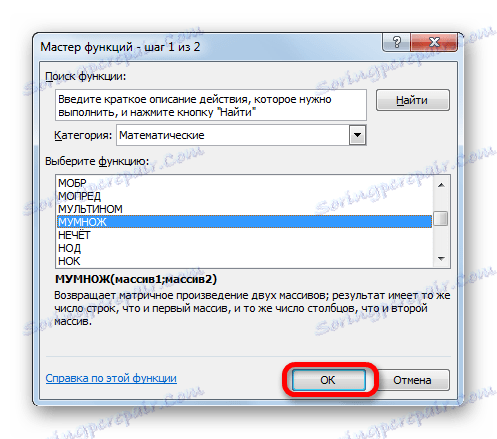
8. U kategoriji "Matematički" , pokrenuti čarobnjak za funkcije , odaberite naziv "LIJEK" i kliknite gumb "OK" .
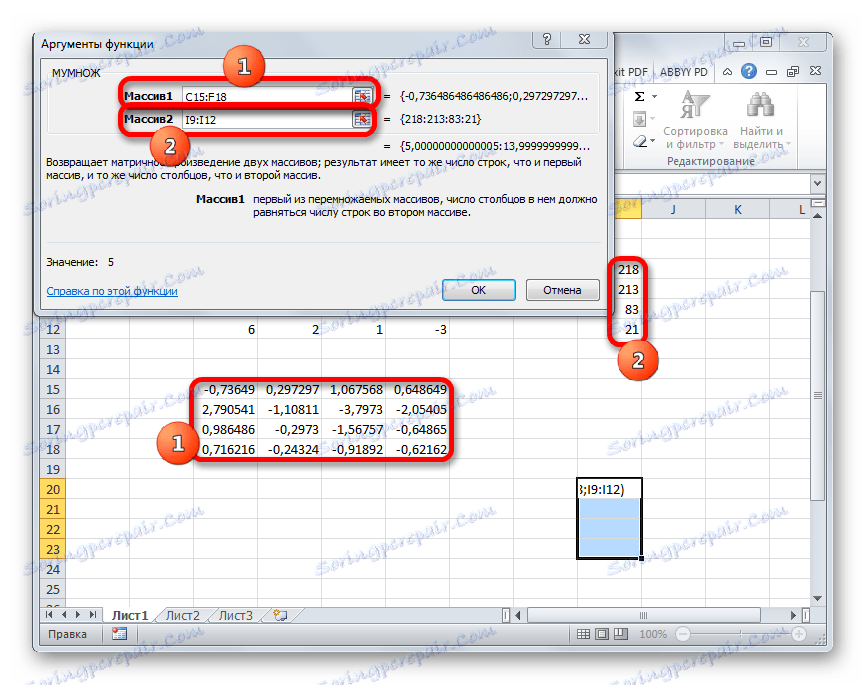
9. Prozor argumenata funkcije MULTI . U polju "Array1" unosimo koordinate naše inverzne matrice. Za to, kao posljednji put, postavljamo pokazivač u polje i pritisnemo lijevu tipku miša, odaberite odgovarajuću tablicu kursorom. Izvršavamo sličnu radnju za unos koordinata u polje "Array2" , samo ovaj put odaberemo vrijednosti stupca B. Nakon što se gore navedene radnje provode, ponovno nemojte žuriti da pritisnete gumb "U redu" ili tipku Enter i upišite Ctrl + Shift + Enter .
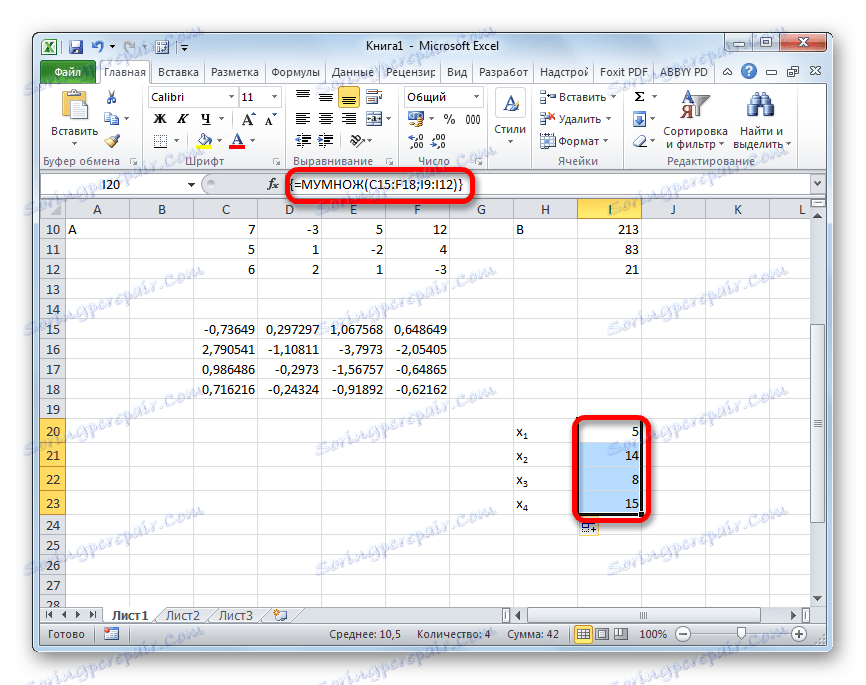
10. Nakon ove akcije, korijeni jednadžbe prikazani su u prethodno odabranoj ćeliji: X1 , X2 , X3 i X4 . Oni će biti raspoređeni uzastopno. Dakle, možemo reći da smo riješili taj sustav. Da bi se potvrdila ispravnost rješenja, dovoljno je zamijeniti ove korijene za izvorni sustav izraza. Ako se promatra jednakost, onda to znači da je prikazani sustav jednadžbi pravilno riješen.

Pouka: Inverzna matrica u programu Excel

Metoda 2: odabir parametara

Drugi poznati način rješavanja sustava jednadžbi u programu Excel je primjena metode odabira parametara. Bit ove metode leži u potrazi za suprotno. Na temelju poznatog rezultata tražimo nepoznat argument. Koristimo kvadratnu jednadžbu

3x^2+4x-132=0

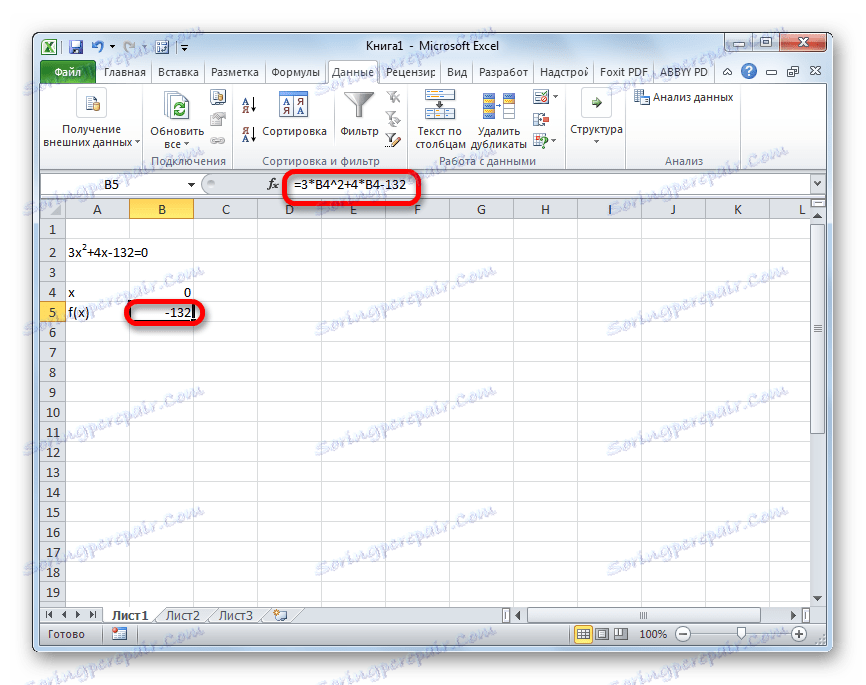
1. Pretpostavimo vrijednost x za jednaku 0 . Izračunavamo odgovarajuću vrijednost f (x) primjenom sljedeće formule:

   =3*x^2+4*x-132

   Umjesto vrijednosti "X", zamijenite adresu ćelije na kojoj se nalazi broj 0 , koji smo uzeli za x .

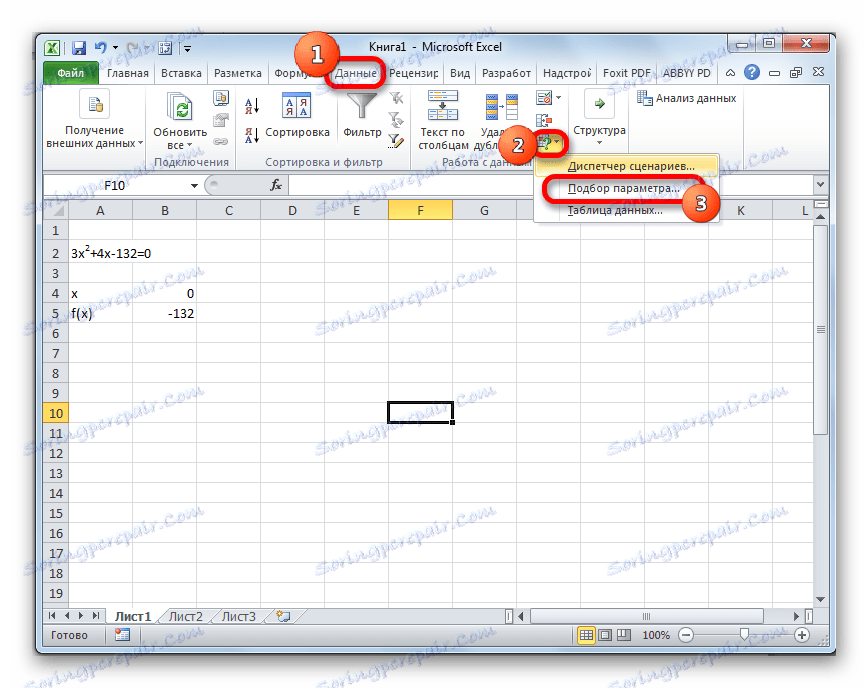
2. Idite na karticu "Podaci" . Kliknite na gumb "Analiza što ako" . Ovaj gumb nalazi se na vrpci u okviru alata "Rad s podacima" . Prikazan je padajući izbornik. U njemu odaberite stavku "Odabir parametara ..." .
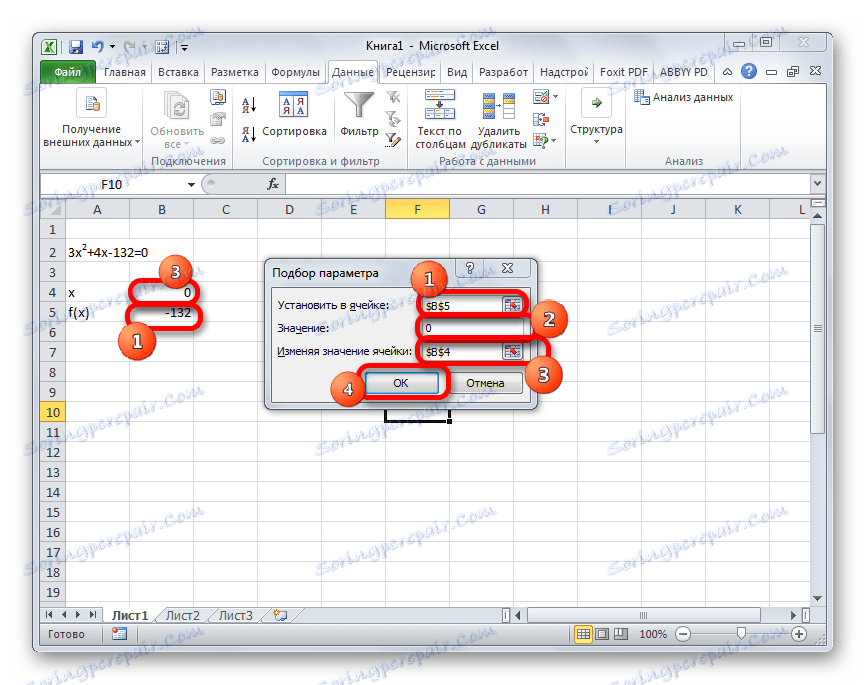
3. Pokreće se prozor za odabir parametara. Kao što vidite, sastoji se od tri polja. U polju "Postavi u ćeliji" navodimo adresu ćelije u kojoj se pronađe formula f (x) , koju smo izmjerili malo prije. U polje "Vrijednost" unesite broj "0" . U polju "Promjena vrijednosti" navodimo adresu ćelije u kojoj se nalazi vrijednost x , koju smo prethodno preuzeli za 0 . Nakon dovršetka ovih koraka pritisnite gumb "OK" .
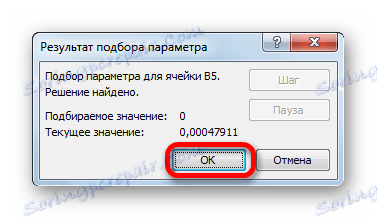
4. Nakon toga, Excel će izvršiti izračun odabirom parametra. To će biti prikazano u prozoru s informacijama koji se pojavio. U njemu kliknite gumb "U redu" .
5. Rezultat izračuna korijena jednadžbe bit će u ćeliji koju smo dodijelili u polju "Promjena vrijednosti" . U našem slučaju, kao što vidimo, x će biti jednak 6 .

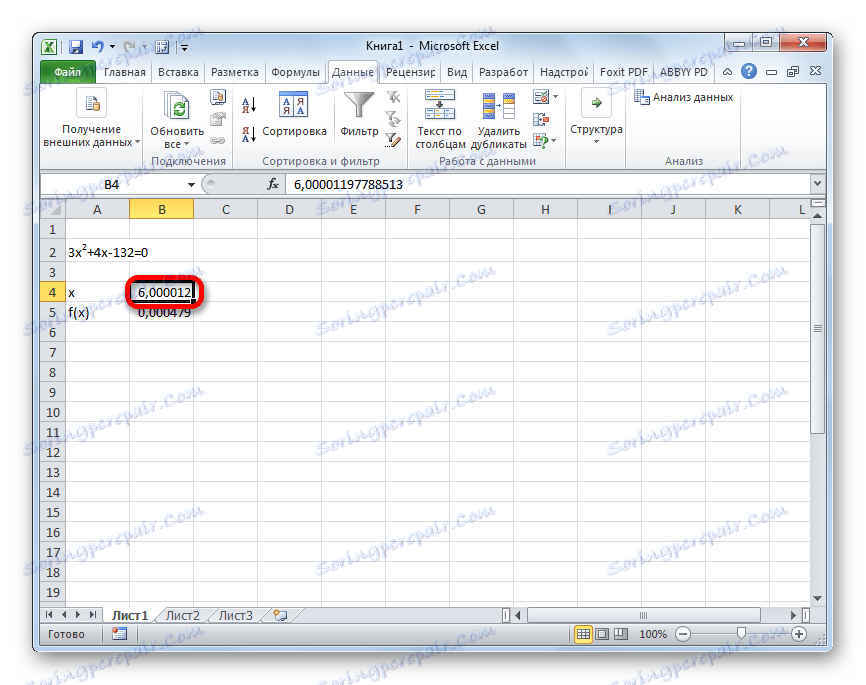
Ovaj rezultat se također može provjeriti zamjenom ove vrijednosti u riješenom izrazu umjesto vrijednosti x .

Pouka: Odabir parametara u programu Excel

Metoda 3: Cramerova metoda

Sada pokušavamo riješiti sustav jednadžbi Cramerovom metodom. Na primjer, uzmite isti sustav koji je upotrijebljen u načinu rada 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


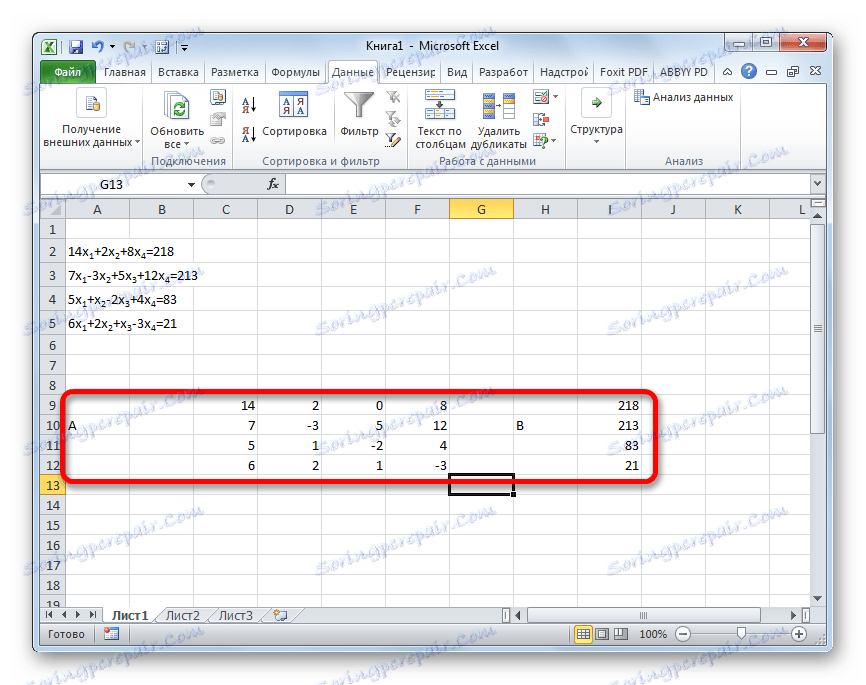
1. Kao u prvoj metodi, sastavljamo matricu A iz koeficijenata jednadžbi i tablice B iz vrijednosti koje stoje iza "jednakog" znaka.
2. Onda napravimo još četiri tablice. Svaka od njih je kopija matrice A , samo za te kopije jedan stupac zamjenjuje se tablicom B naizmjence. Prva tablica ima prvi stupac, druga tablica ima drugi stupac i tako dalje.
3. Sada moramo izračunati determinante za sve te tablice. Sustav jednadžbi imat će rješenja samo ako sve odrednice imaju vrijednost različitu od nule. Da biste ponovno izračunali ovu vrijednost u programu Excel, postoji zasebna funkcija - MOPRED . Sintaksa ovog operatora je:

   =МОПРЕД(массив)

   Dakle, kao u slučaju MBD funkcije, jedini argument je referenca na obrađujuću tablicu.

   Dakle, odaberite ćeliju u kojoj će biti prikazana odrednica prve matrice. Zatim kliknite gumb "Umetni funkciju" , koji je poznat iz prethodnih metoda.

4. Aktiviran je prozor čarobnjake . Prešli smo u kategoriju "Matematički" i među popisom operatora odabiremo ime "MOPRED" . Nakon toga kliknite gumb "U redu" .
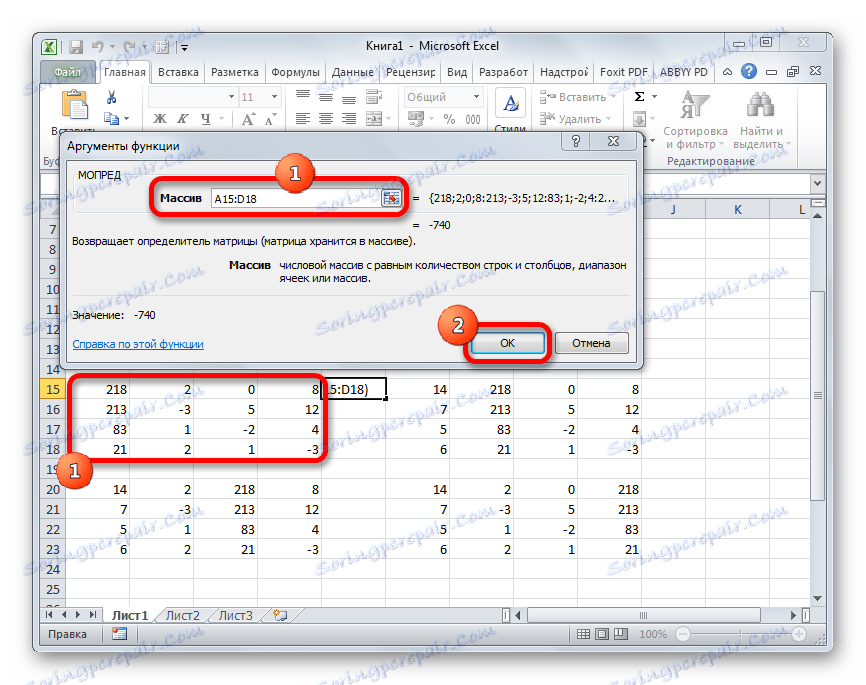
5. Pokrenut je prozor s argumentima funkcije MOPED . Kao što možete vidjeti, ima samo jedno polje - "Array" . U ovom polju unosimo adresu prve transformirane matrice. Da biste to učinili, postavite pokazivač u polje, a zatim odaberite raspon matrice. Nakon toga kliknite gumb "U redu" . Ova funkcija izlaže rezultat u jednoj ćeliji, a ne polju, tako da ne morate pritisnuti Ctrl + Shift + Enter da biste dobili izračun.
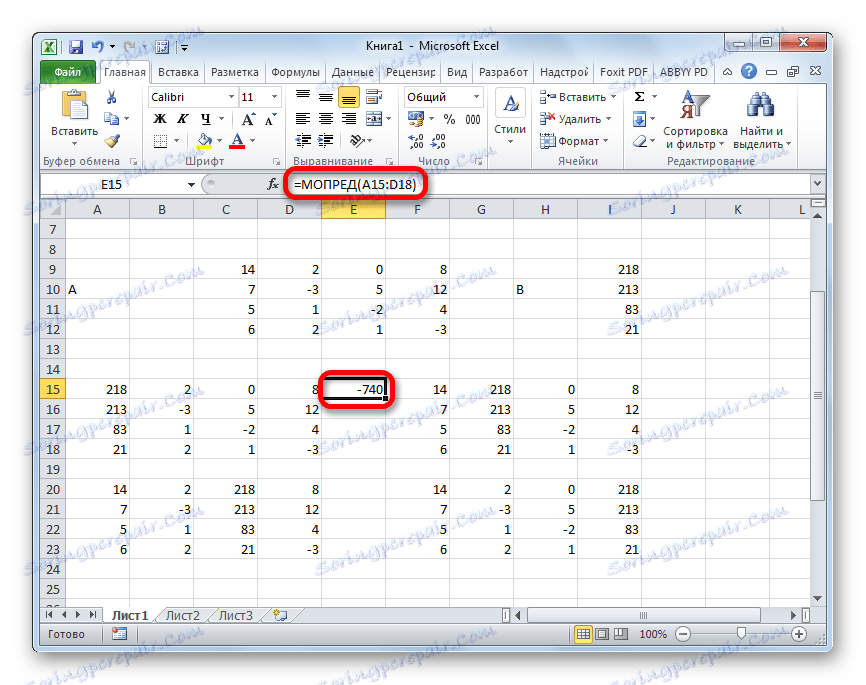
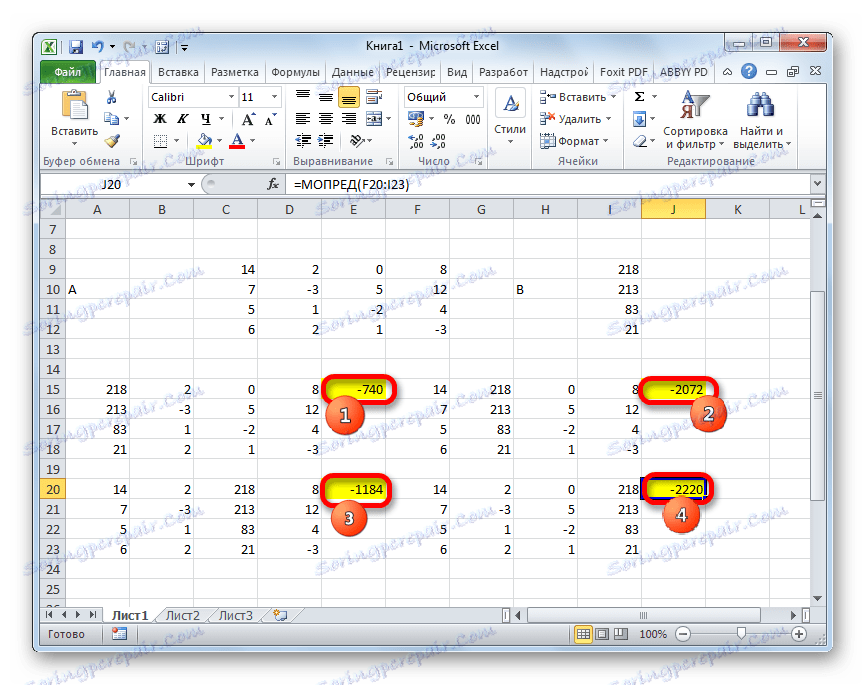
6. Funkcija izračunava rezultat i izlazi na prethodno odabranu ćeliju. Kao što možete vidjeti, u našem je slučaju determinanta -740 , to jest, nije jednak nuli, što je pogodno za nas.
7. Isto tako izračunavamo determinante za preostala tri tablica.
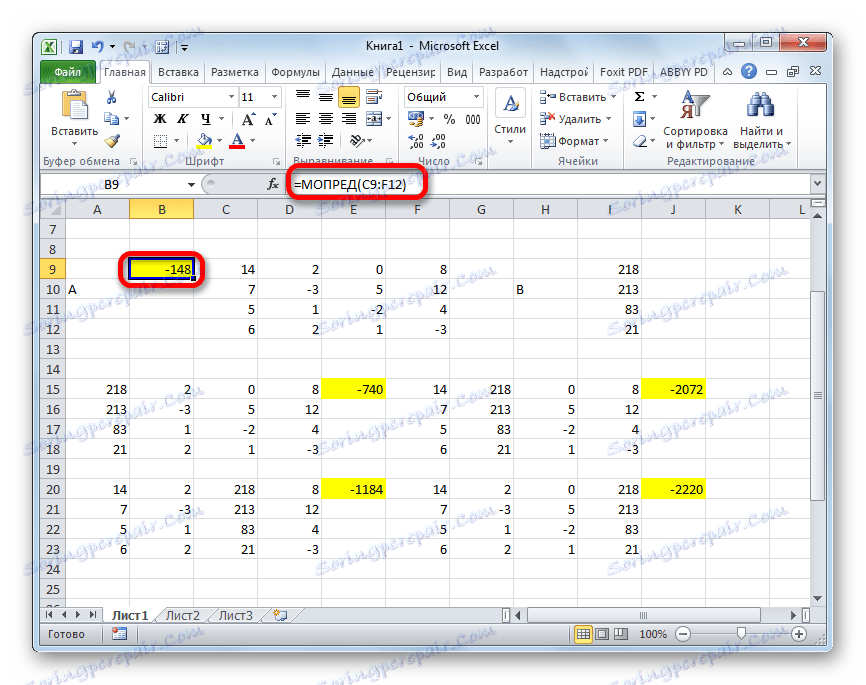
8. U završnoj fazi izračunavamo determinanta primarne matrice. Postupak je isti za isti algoritam. Kao što možete vidjeti, determinanta primarne tablice također se razlikuje od nule, pa se matrica smatra neregeneriranom, tj. Sustav jednadžbi ima rješenja.
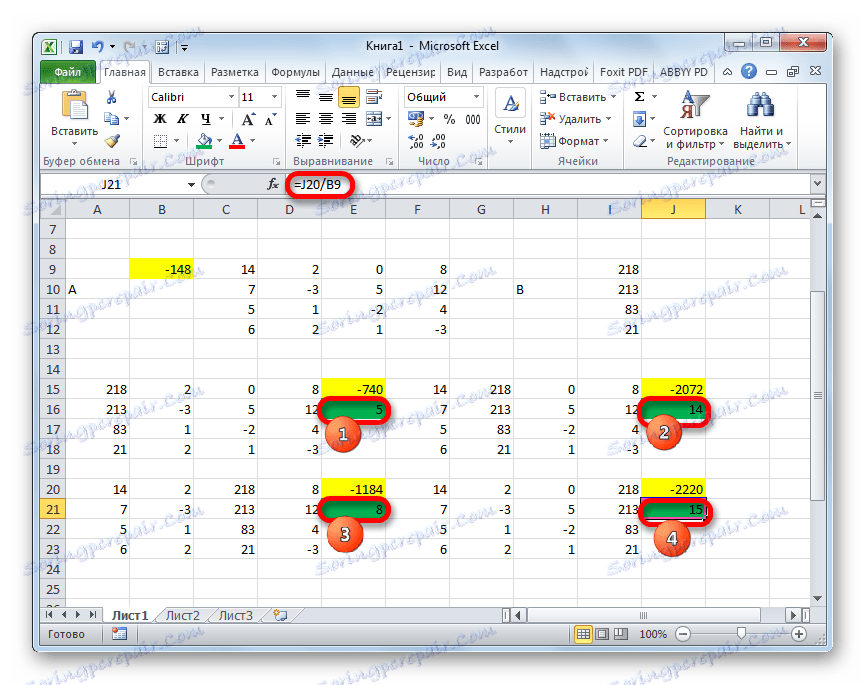
9. Sada je vrijeme da nađemo korijene jednadžbe. Korijen jednadžbe bit će jednak omjeru determinante odgovarajuće transformirane matrice prema determinanti primarne tablice. Dakle, nakon što smo podijelili sve četiri determinante transformiranih matrica jedan po jedan -148 , što je odrednica izvornog stola, dobivamo četiri korijena. Kao što možete vidjeti, oni su jednaki vrijednostima 5 , 14 , 8 i 15 . Dakle, oni se podudaraju s korijenima koji smo pronašli pomoću inverzne matrice u metodi 1 , što potvrđuje ispravnost rješenja sustava jednadžbi.

Metoda 4: Gaussova metoda

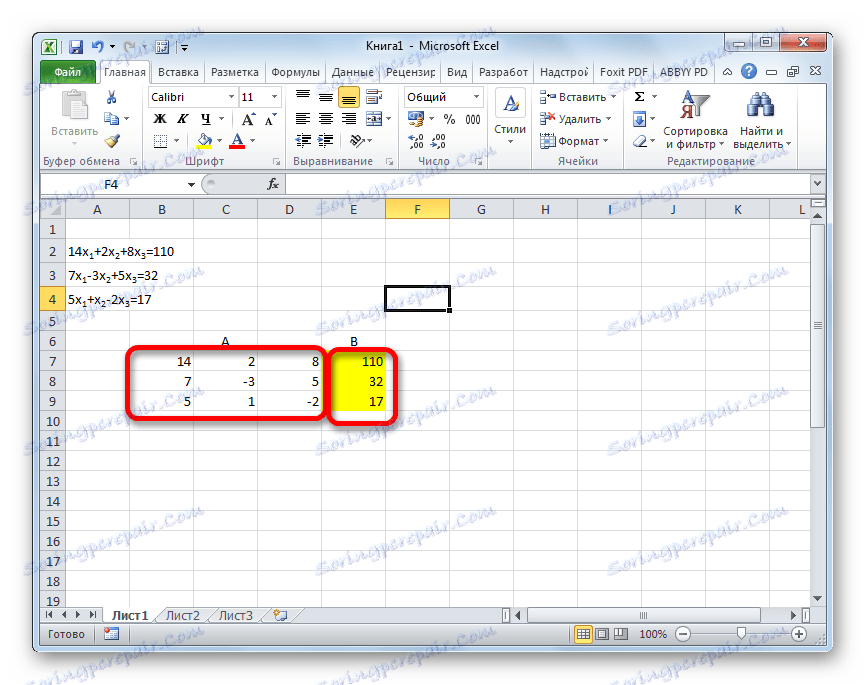
Rješavanje sustava jednadžbi se također može obaviti pomoću Gauss metode. Na primjer, uzmimo jednostavniji sustav jednadžbi od tri nepoznanice:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


1. Ponovno uspoređujemo koeficijente u tablici A i slobodni termini koji se nalaze nakon znaka "jednako" u tablici B. Ali ovaj put ćemo približiti obje stolice, jer će nam to biti potrebno da radimo u budućnosti. Važan uvjet je da se u prvoj ćeliji matrice A vrijednost razlikuje od nule. U suprotnom slučaju, trebali biste preurediti retke na mjestima.
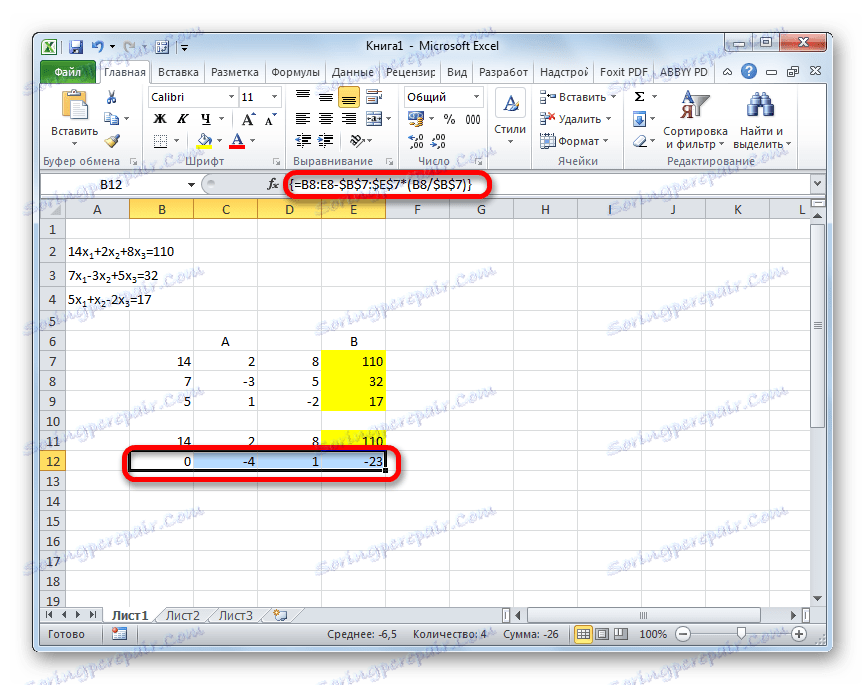
2. Kopirajte prvi red dva povezana matrica u retku ispod (za jasnoću, možete preskočiti jedan redak). U prvoj ćeliji, koja se nalazi u redu čak niža od prethodnog, unosimo sljedeću formulu:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Ako drugačije uređujete matrice, adrese stanice formule imaju različite vrijednosti, ali ih možete izračunati usporedbom s formulama i slikama koje su ovdje navedene.

   Nakon unosa formule, odaberite cijeli red ćelija i pritisnite Ctrl + Shift + Enter . Formula polja primijenit će se na red i ispunit će vrijednosti. Tako smo oduzeli od druge linije prvi, pomnožen omjerom prvog koeficijenata prva dva izraza sustava.

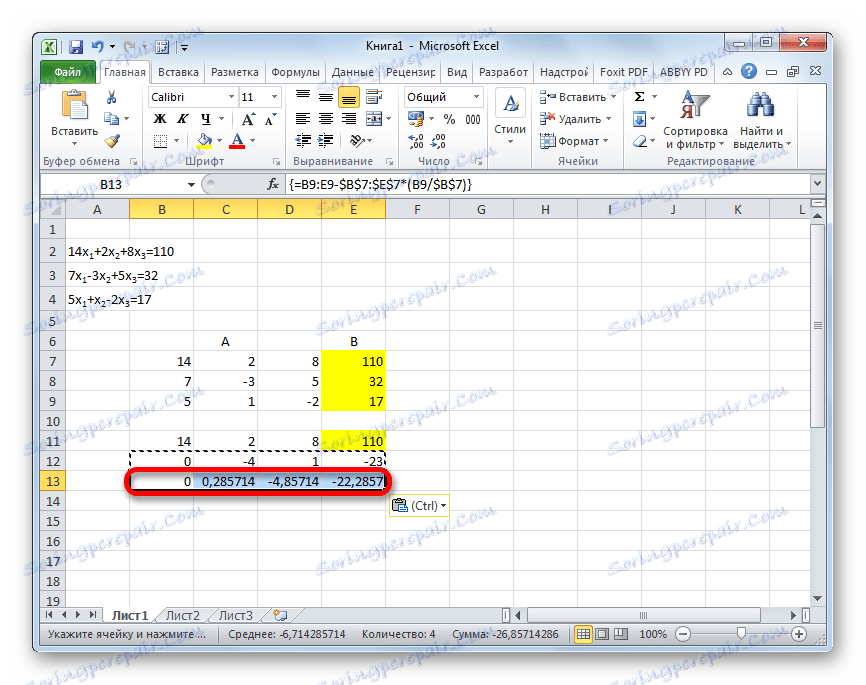
3. Nakon toga kopirajte rezultirajuću liniju i zalijepite je u donju liniju.
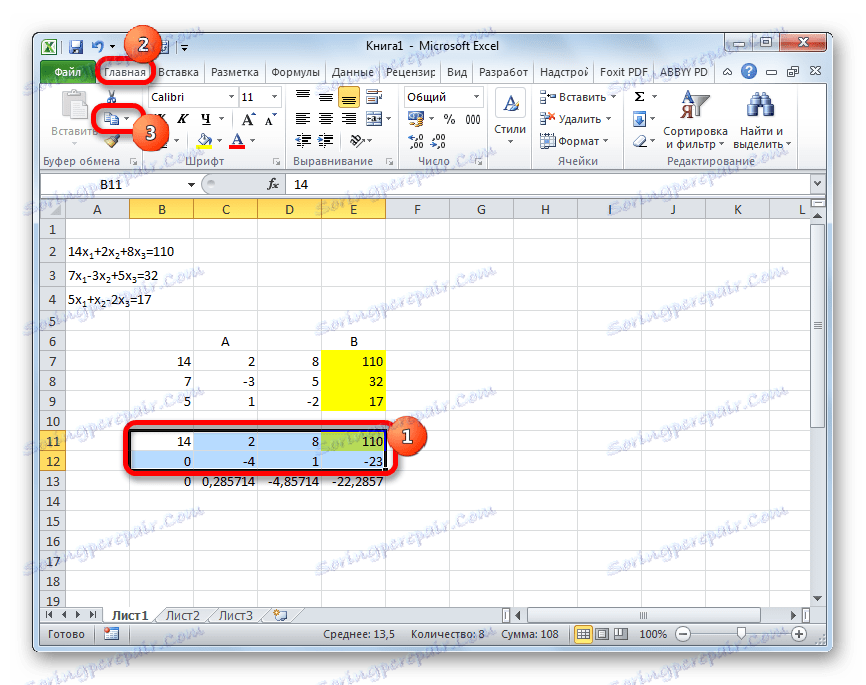
4. Odaberite prva dva retka nakon nedostajuće linije. Kliknite gumb "Kopiraj" koji se nalazi na vrpci na kartici "Početna" .
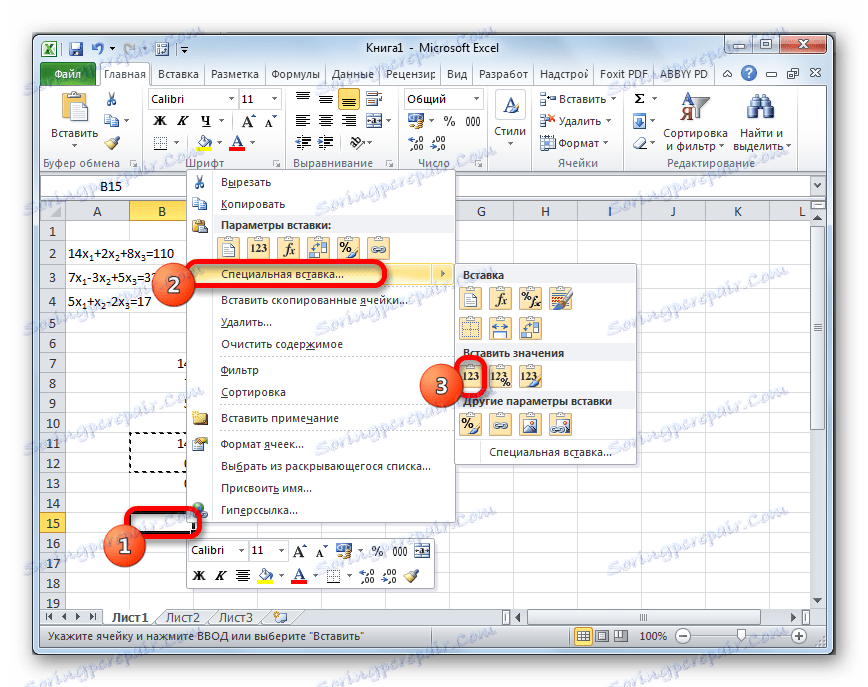
5. Preskočimo liniju nakon posljednjeg zapisa na listi. Odaberite prvu ćeliju u sljedećem retku. Kliknite desnom tipkom miša. U otvorenom kontekstnom izborniku mišemo kursorom iznad stavke "Posebna lijepljenje" . Na dodatnom popisu koji počinje, odaberite stavku "Vrijednosti" .
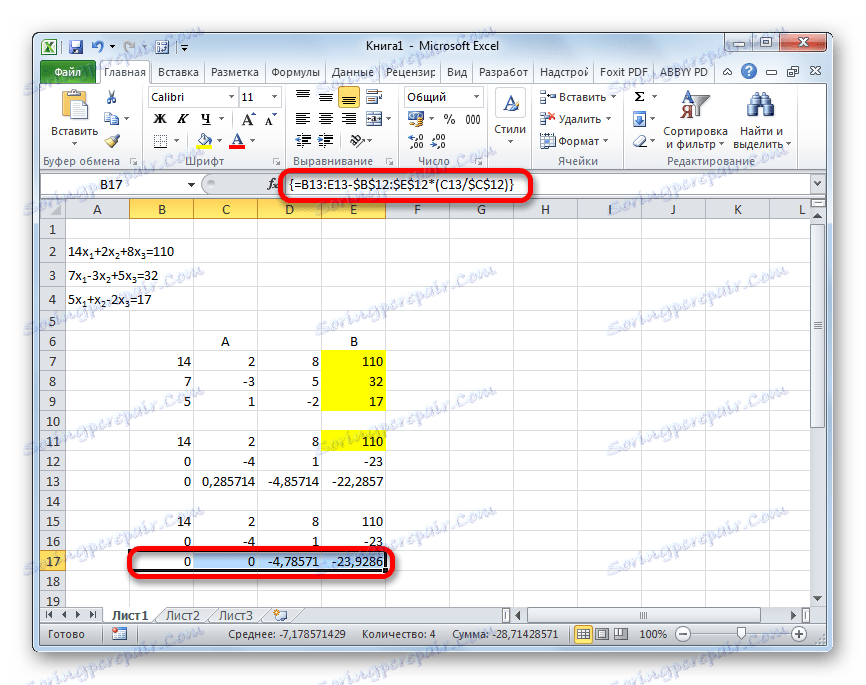
6. U sljedećem retku unesite formulu polja. Oduzima drugi redak iz trećeg retka prethodne grupe podataka, pomnožen s omjerom drugog koeficijenta trećeg i drugog reda. U našem slučaju, formula će imati sljedeći oblik:

   =B13:E13-$B$12:$E$12*(C13/$C$12)

   Nakon ulaska u formulu odaberite cijelu seriju i primijenite tipkovnički prečac Ctrl + Shift + Enter .

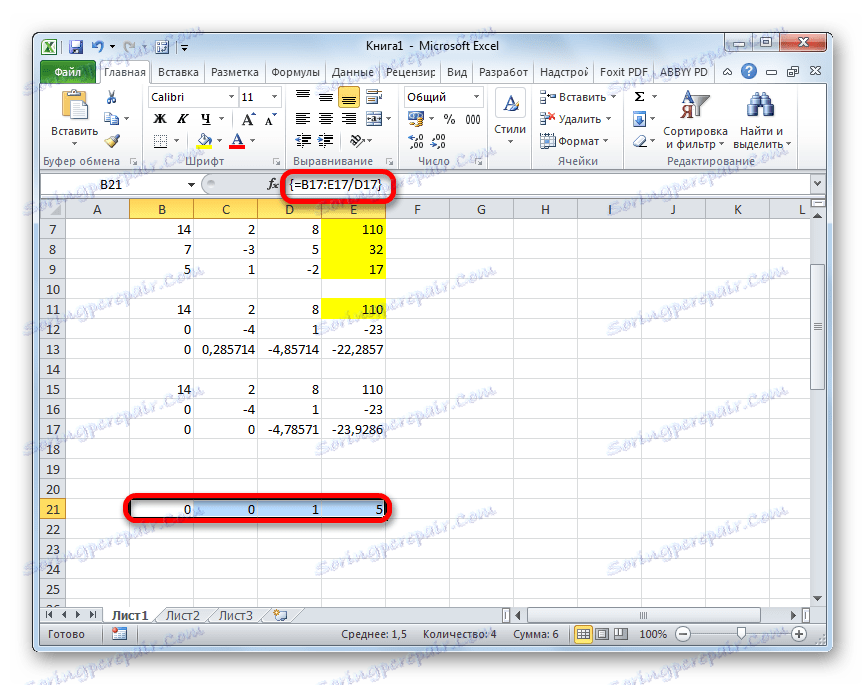
7. Sada je potrebno izvršiti obrnuti smjer pomoću Gaussove metode. Preskočimo tri retka od zadnjeg zapisa. U četvrtoj liniji unosimo formulu polja:

   =B17:E17/D17

   Dakle, podijelimo posljednju liniju koju izračunamo njegovim trećim koeficijentom. Nakon što upišete formulu, odaberite cijelu liniju i pritisnite Ctrl + Shift + Enter .

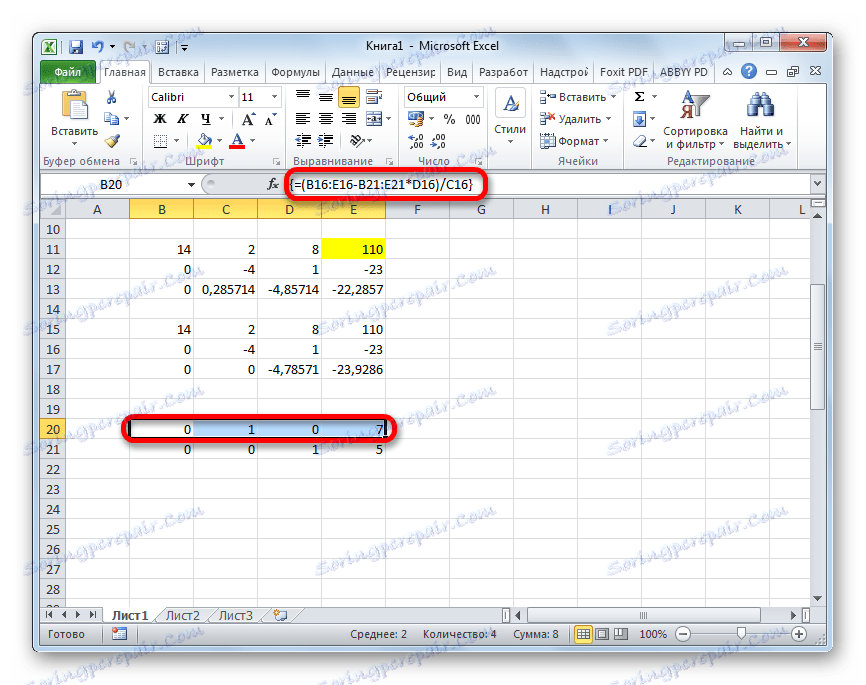
8. Uspijevamo na liniji prema gore i ulazimo u nju sljedeću formulu polja:

   =(B16:E16-B21:E21*D16)/C16

   Pritiskamo uobičajenu kombinaciju tipki za primjenu formule polja.

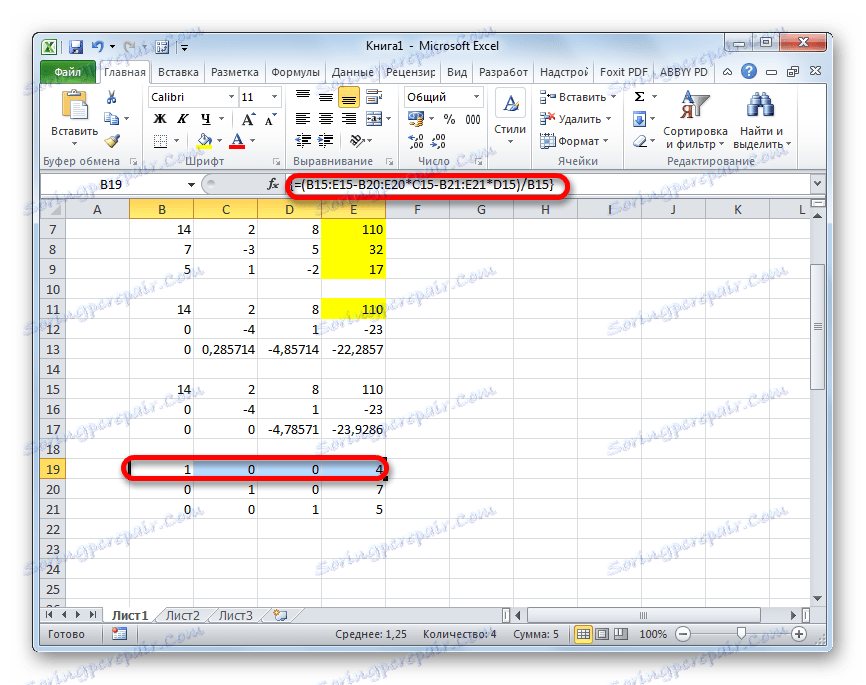
9. Podižemo još jednu liniju veću. U njemu ulazimo formulu polja sljedećeg oblika:

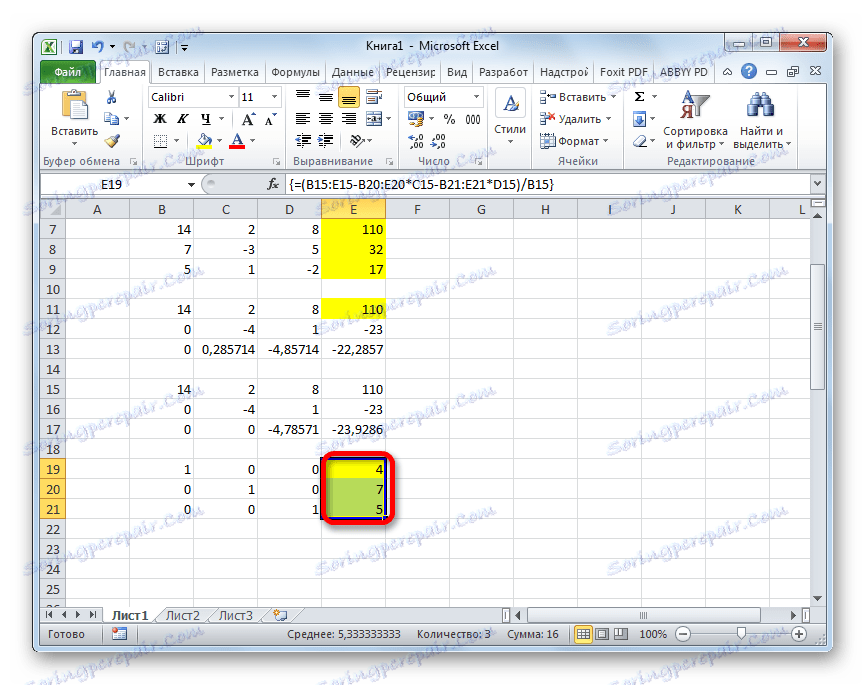
   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Ponovno odaberite cijelu liniju i primijenite kombinaciju tipki Ctrl + Shift + Enter .

10. Sada pogledajte brojeve koji su dobiveni u zadnjem stupcu posljednjeg bloka linija, koji smo ranije izračunali. To su ti brojevi ( 4 , 7 i 5 ) koji će biti korijeni datog sustava jednadžbi. To možete provjeriti zamjenom umjesto X1 , X2 i X3 u izrazima.

Kao što možete vidjeti, u sustavu jednadžbi sustava Excel može se riješiti nizom metoda, od kojih svaki ima svoje prednosti i nedostatke. Ali sve te metode mogu se uvjetno podijeliti u dvije velike skupine: matricu i upotrebu alata za odabir parametara. U nekim slučajevima metode ne uvijek metode matrice prikladne su za rješavanje problema. Konkretno, kada je determinanta matrice nula. U drugim slučajevima, korisnik može slobodno odlučiti koju opciju smatra prikladnijim za sebe.

• ← Izgradnja parabole u Microsoft Excelu
• Izrada gumba u programu Microsoft Excel →