nadmašiti

Primjena metode najmanjeg kvadrata u programu Excel

Metoda najmanjih kvadrata je matematički postupak za konstruiranje linearne jednadžbe koja bi najpreciznije odgovarala skupu dviju serija brojeva. Svrha ove metode je minimizirati ukupnu kvadratnu pogrešku. U programu Excel postoje alati pomoću kojih možete primijeniti ovu metodu u svojim proračunima. Pogledajmo kako je to učinjeno.

Korištenje metode u programu Excel

Metoda najmanjih kvadrata (OLS) je matematički opis ovisnosti jedne varijable na drugom. Može se koristiti za predviđanje.

Omogućivanje rješenja za dodavanje na popisu

Da biste koristili OLS u programu Excel, morate omogućiti dodatak "Pronađi rješenje" koji je prema zadanim postavkama onemogućen.

  1. Idite na karticu "Datoteka" .

    2. Idite na karticu Datoteka u programu Microsoft Excel

  2. Kliknemo na naziv odjeljka "Parametri" .

    3. Idite na opcije u programu Microsoft Excel

  3. U prozoru koji se otvori zaustavljamo odabir pododjeljka "Dodaci" .

    4. Idite na pododjeljak dodatka u programu Microsoft Excel

  4. U bloku "Upravljanje" , koji se nalazi na dnu prozora, postavite prebacivanje na poziciju "Excel dodatke" (ako ima drugačiju vrijednost) i kliknite gumb "Idi ..." .

    5. Idite na Excel dodatke u programu Microsoft Excel

  5. Otvara se mali prozor. Stavili smo kvačicu o parametru "Pronalaženje rješenja" . Kliknite gumb "OK" .

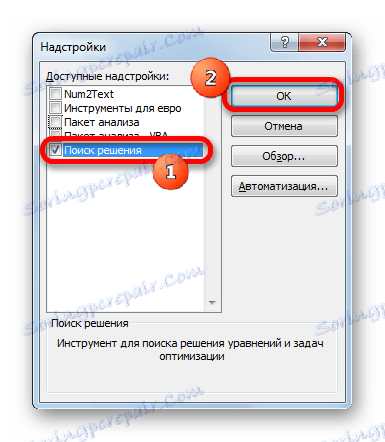
Omogućavanje pretraživanja rješenja u Microsoft Excelu

Sada je omogućena funkcija Pronađi rješenje u programu Excel i alati se pojavljuju na vrpci.

Pouka: Pretraživanje rješenja u programu Excel

Uvjeti zadataka

Opišimo primjenu OLS-a na konkretan primjer. Imamo dva reda brojeva x i y , čiji slijed je prikazan na donjoj slici.

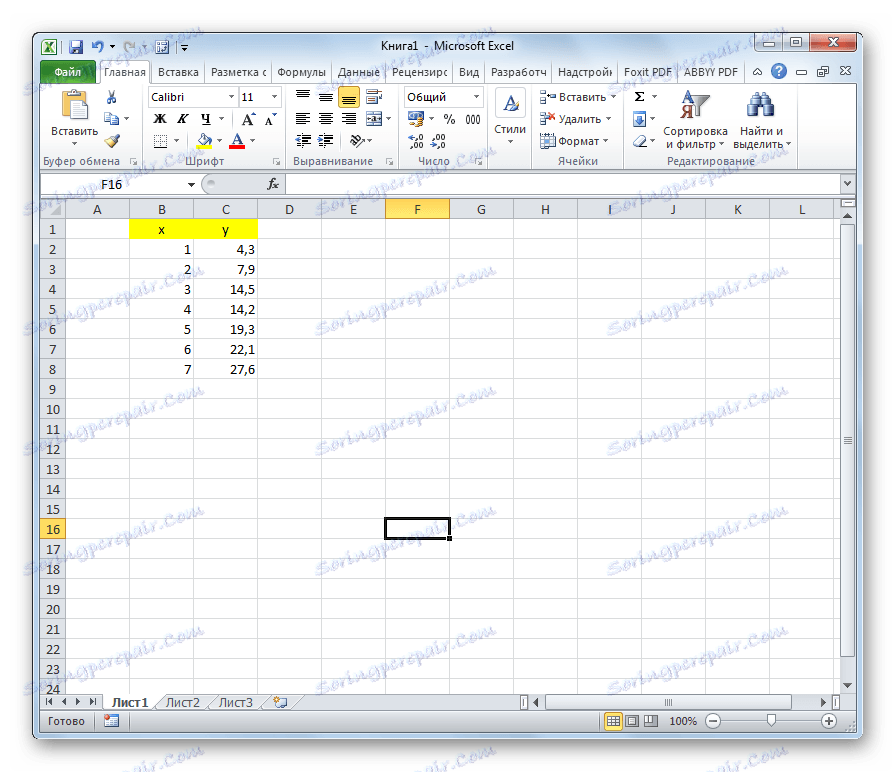
Varijable u programu Microsoft Excel

Funkcija najbolje može opisati ovu ovisnost:

y=a+nx

U ovom slučaju, poznato je da za x = 0, y je također 0 . Dakle, ova jednadžba može se opisati ovisnošću y = nx .

Moramo pronaći minimalni zbroj kvadrata razlike.

Rješenje

Sad ćemo opisati izravnu primjenu metode.

  1. Lijevo od prve vrijednosti x stavili smo broj 1 . Ovo je približna vrijednost prve vrijednosti koeficijenta n .

    2. Vrijednost koeficijenta n u Microsoft Excelu

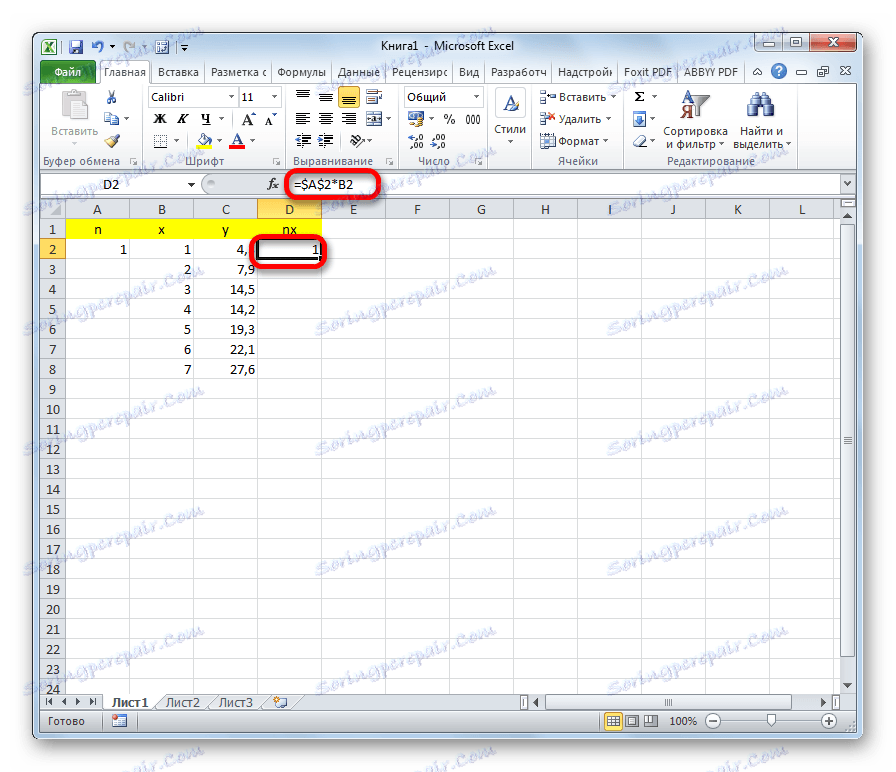
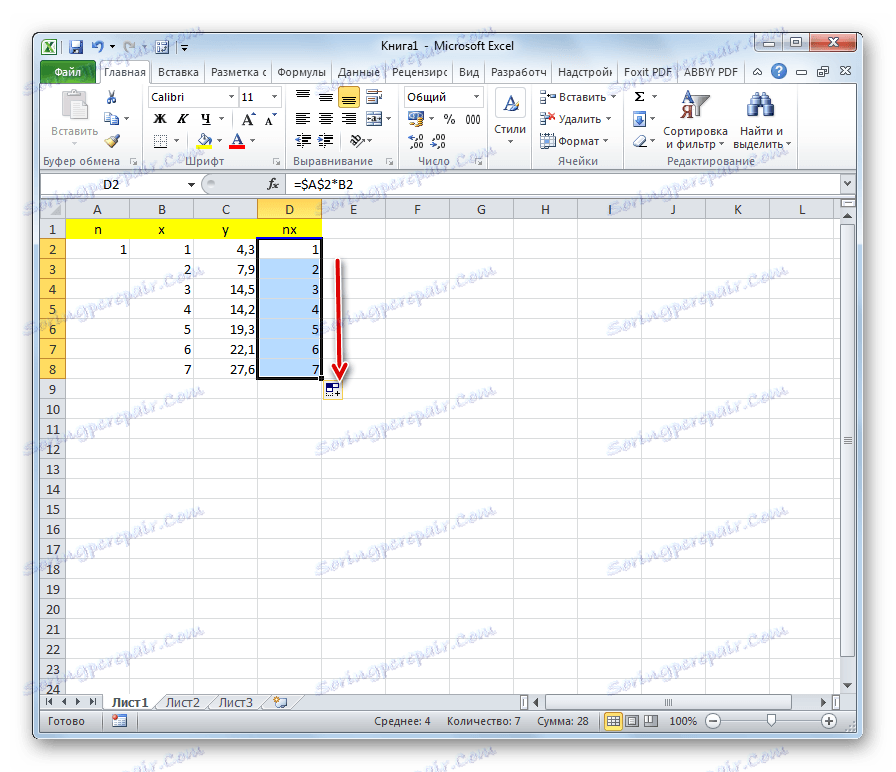
  2. Desno od stupca y dodajte još jedan stupac - nx . U prvoj ćeliji ovog stupca zapisujemo formulu za umnožavanje koeficijenta n pomoću ćelije prve varijable x . Istodobno se obavlja veza na polje s koeficijentom apsolutan , jer se ta vrijednost neće promijeniti. Kliknite gumb Enter .

    3. Vrijednost nx u Microsoft Excelu

  3. koristeći oznaka za ispunjavanje , kopirajte ovu formulu na cijeli raspon tablice u donjem stupcu.

    4. Kopiranje formule u Microsoft Excel

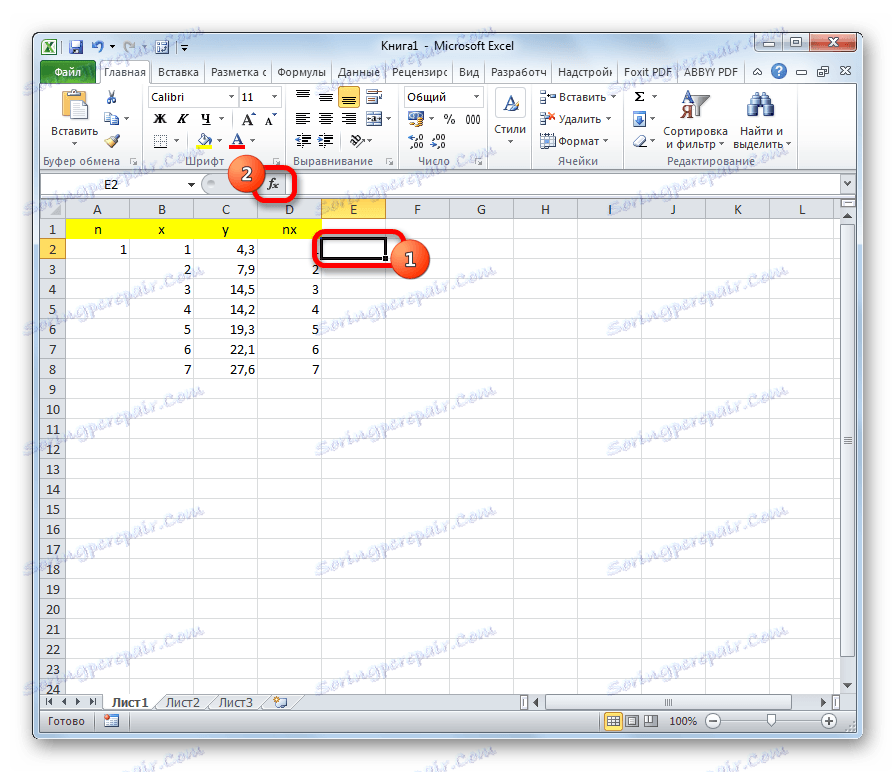
  4. U zasebnoj ćeliji, izračunajte zbroj razlika kvadrata vrijednosti y i nx . Da biste to učinili, kliknite gumb "Umetni funkciju" .

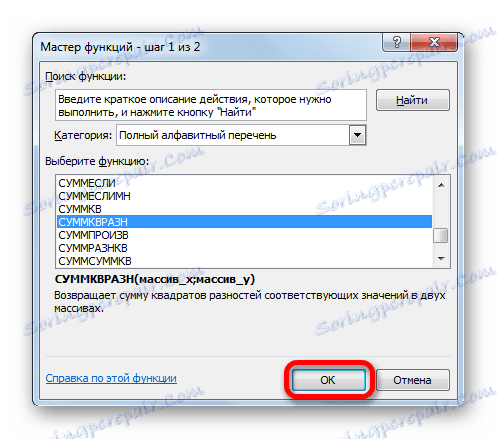
    5. Idite na čarobnjak za funkcije u programu Microsoft Excel

  5. U otvorenom "Čarobnjak za funkcije" tražimo unos "SUMMKVRAZN" . Odaberite ga i kliknite gumb "U redu" .

    6. Čarobnjak za funkcije u programu Microsoft Excel

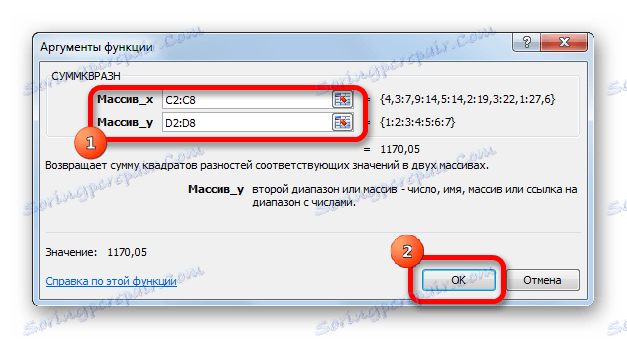
  6. Otvara prozor argumenata. U polju "Array_x" unosimo raspon ćelija stupca y . U polju "Array_y" unosimo raspon ćelija stupca nx . Da biste unijeli vrijednosti, jednostavno postavite pokazivač u polje i odaberite odgovarajući raspon na listu. Nakon unosa, pritisnite gumb "OK" .

    7. Unos funkcijskih argumenata u Microsoft Excel

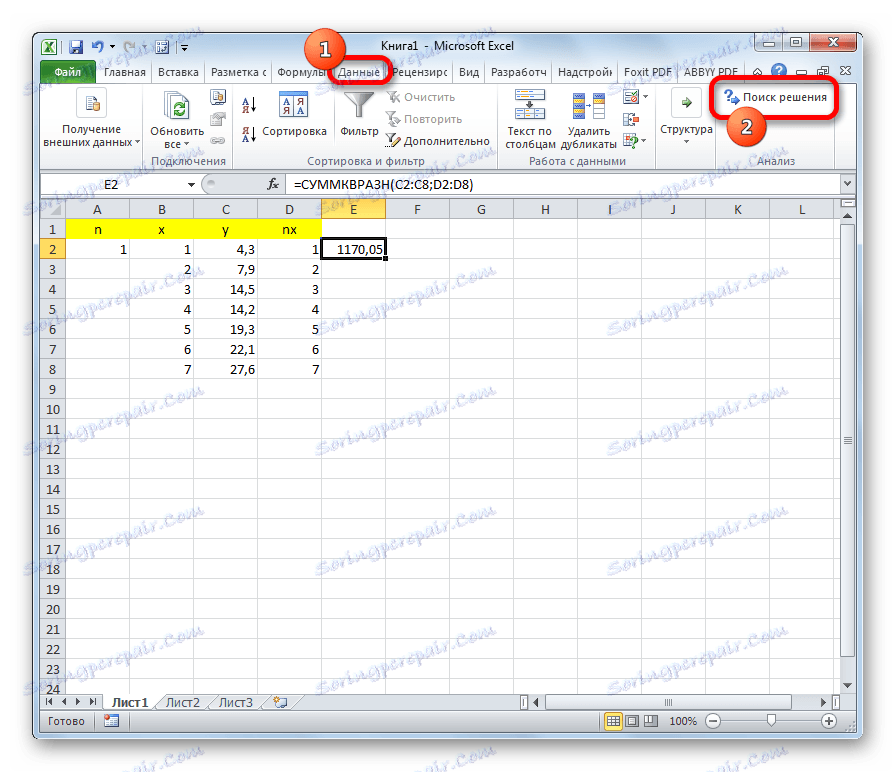
  7. Idite na karticu "Podaci" . Na vrpci u alatu "Analiza" kliknite gumb "Pronađi rješenje" .

    8. Idite na pretraživanje rješenja u Microsoft Excelu

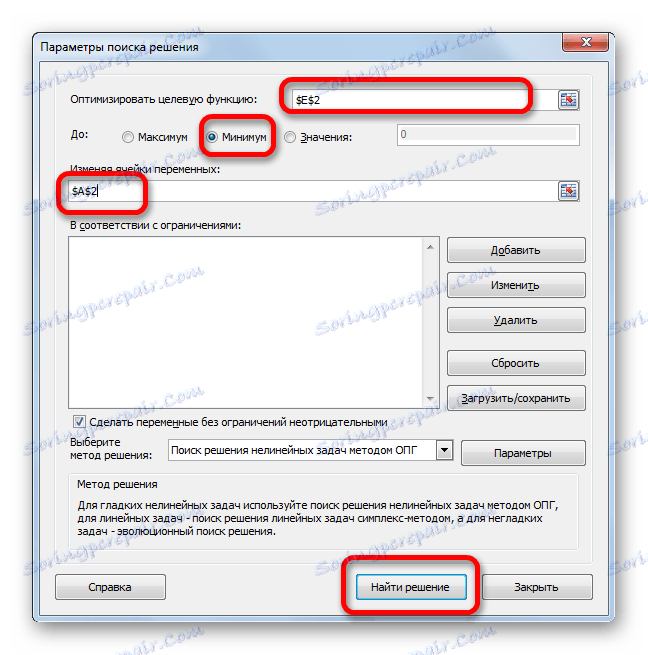
  8. Otvara se prozor parametara za ovaj alat. U polju "Optimiziraj ciljnu funkciju" navodimo adresu ćelije s formulom "SUMMKVRAZN" . U parametru "To" moramo postaviti prekidač na "Minimalni" položaj. U polju "Promjena ćelija" navodimo adresu s vrijednošću koeficijenta n . Kliknite gumb "Pronađi rješenje" .

    9. Pronalaženje najmanjih kvadratnih rješenja u Microsoft Excelu

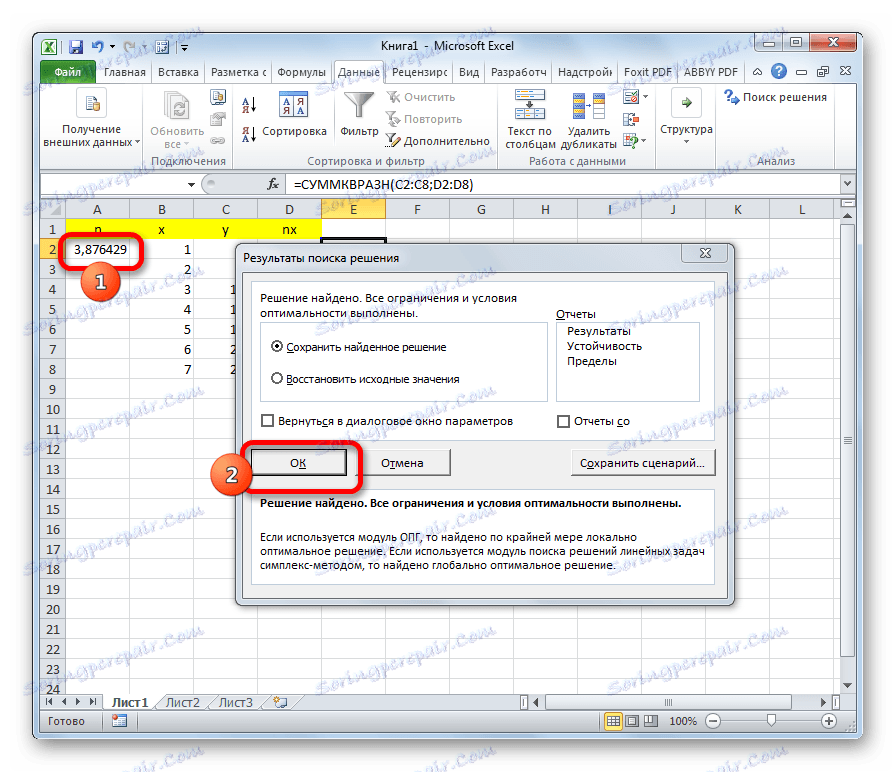
  9. Rješenje će biti prikazano u ćeliji koeficijenta n . To je ta vrijednost koja će biti najmanji kvadrat funkcije. Ako rezultat zadovoljava korisnika, kliknite gumb "U redu" u dodatnom prozoru.

Potvrdite rezultat u programu Microsoft Excel

Kao što vidimo, primjena metode najmanjeg kvadrata je prilično složen matematički postupak. Pokazali smo to u akciji na najjednostavniji primjer, a mnogo je složenijih slučajeva. Međutim, alat za Microsoft Excel dizajniran je kako bi se proračuni pojednostavnili što je više moguće.